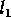 ..
..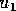 [by
[by 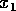 ],
], 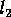 ..
..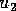 [by
[by 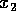 ], ...,
], ..., 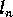 ..
..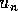 [by
[by 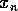 ]}
]}[with imap <imap-name>];
set <set-name> = {..
[by
],
..
[by
], ...,
..
[by
]}
[with imap <imap-name>];
We will discuss the concept of imap shortly. set is the
keyword signalling set definition.
set-name is the
user selected name of the set, 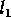 ,
, 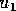 ,
, 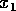 ,
,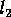 ,
,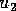 ,
,
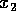 ,...,
,...,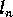 ,
,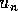 ,
,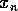 are required
to be integers given as explicit constants. The terminology is:
are required
to be integers given as explicit constants. The terminology is:
is called the lower limit of dimension
.
is called the upper limit of dimension
.
specifies the increment to be used while enumerating the range specified by li and ui, the default increment being 1.
(-
)/
will give the size of dimension
.
Thus one can
specify a set consisting of elements 1 through 101 with the
construct
set onetoomany = { 1..101 };where set is the keyword signalling a set definition. Since sets normally consists of process-identifiers, the user may choose to have a set that includes every third process. This can be done with
set everythird = { 1..101 by 3};
Often programmers form a logical n-dimensional grid on a
set physical processors. When instrumentation is done at run-time,
the process identifiers are single integers, from which different
dimensional indices are computed by the user. Ariadne allows the user
to use the logical view of the n-dimensional co-ordinate system.
The user needs to specify the relation that will map such logical
n-dimensional co-ordinates to the process-identifier specified in the
trace. This mapping can be specified by through index-mappings. The
syntax of index-mappings is:
imap <imap-name> = <expr> ;where imap is a keyword signalling index mapping definition, imap-name is the name given to this expression by the user, and expr is any arithmetic expression that describes the mapping.
For instance,
imap X = index1*10 + index2;provides one way of mapping elements of two-dimensional sets to the process identifiers. index1, index2 etc are all reserved words, only to be used in the context of index mappings.
imap Y = index1*10 + index2*5 + index3 + index4;
Thus the user can specify a two dimensional set as
set 2Dset = { 1..10, 1..10 } with imap X;
The second way of specifying sets is through combining one or more
defined sets. The syntax is:
set <set-name> = <set-expr> [with <imap-name>];
where set-name is the user-defined name of the new set. set-expr is any arithmetic expression where the identifiers are pre-defined sets and the operators are restricted to union, section (meaning intersection) and cross (meaning cartesian product).
For instance, we can define two sets A and B as:
set A = {0..10, 0..10} with imap X;
set B = {0..10, 5..15} with imap X;
and then use them to define new sets
set Union2d = A union B with imap X;
set Inter2d = A section B with imap X;
set Cross4d = A cross B with imap Y;
The default index mapping is the identity mapping, which is only meaningful for one-dimensional sets. If index mapping is not specified during set definition, the current index mapping is used during run-time to resolve the set elements. Note no error checking is performed: a 3-dimensional set may have an index mapping that only involves two indices and so on.